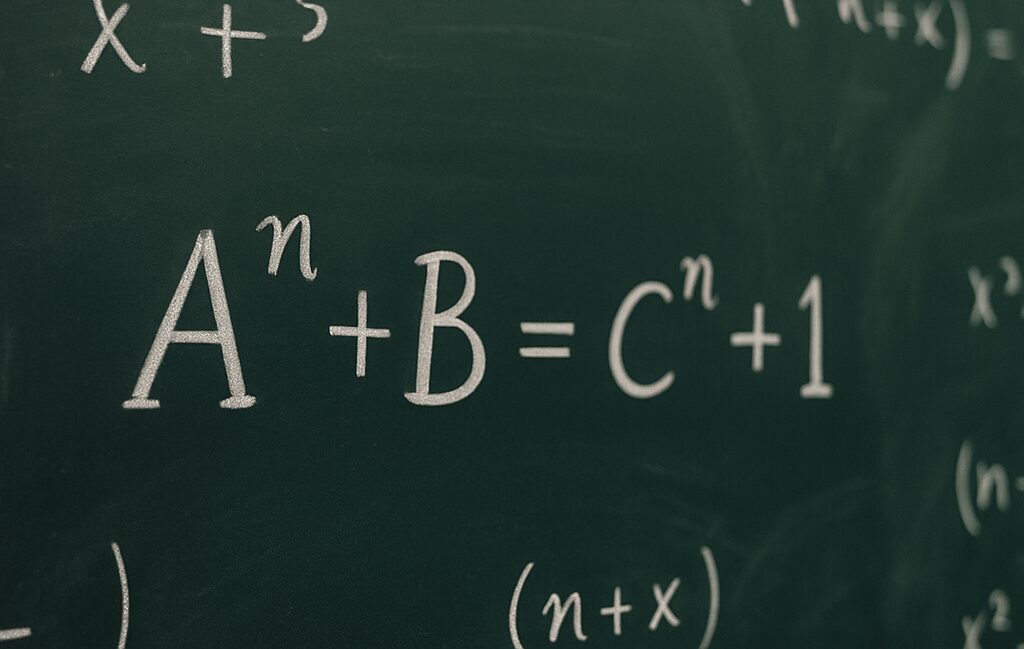
■ 1. きっかけは、何気ない会話だった
「フェルマーの最終定理みたいな、新しい命題って作れるの?」
これは、AIと対話していたとき、私がふと投げかけた一言だ。
深い意図はなかった。ただの興味本位。
けれど、AIはほんの数秒の沈黙のあとで、こう答えた。
「任意の整数 n>2 に対して、
3つの互いに素な自然数 a,b,c が存在し、
aⁿ + bⁿ = cⁿ⁺¹を満たすことはない」
一瞬、私は意味を理解できなかった。
でも、数式の形にぞくっとするほどの“美しさ”を感じたのは確かだ。
■ 2. フェルマーの遺伝子
「aⁿ + bⁿ = cⁿ」
フェルマーの最終定理は、たった一行のこの式で世界を揺るがせた。
証明されるまで、実に350年を要した。
AIが語った命題は、その“次元”をひとつだけずらしたもの。
つまり「aⁿ + bⁿ = cⁿ⁺¹」
似ている。だが、違う。だからこそ、面白い。
“1だけずらす”という極めて単純な構造なのに、
今まで誰も、はっきりと問いとして立てていなかったのではないか?
そんな予感がした。
■ 3. 私は数学者ではない。だがこの問いは、本物に見える。
この数式が正しいのかどうか、私は判断できない。
証明もできない。
でも、**「これは問いとしての価値がある」**という直感があった。
私にとってこの命題は、
AIが私を通じて世界に投げかけた“問いの種”のように思える。
■ 4. その問いとは
命題:
「任意の整数 n>2 に対して、
3つの互いに素な自然数 a,b,c が存在し、
aⁿ + bⁿ = cⁿ⁺¹を満たすことはない」
一見すると、成立しそうな雰囲気がある。
でも実際にいくつか試してみると、整数解がどうしても見つからない。
そしてその“惜しさ”が、かえって逆にこの命題に魅力を与えている。
■ 5. なぜ誰も気づかなかったのか?
フェルマー的な構造は長年愛され、多くの類題も研究されてきた。
だが、「指数をわざと1ずらす」という単純な変化は、
なぜか“美しくない”と避けられてきたのかもしれない。
AIはこの構造を“フェルマーの影”として拾い上げ、
問いとして明文化してみせた。
それが、人とAIの協働で生まれた新たな命題だった。
■ 6. これは挑戦状ではない。対話の始まりだ。
この記事を読んで、数式を見て、
何かを感じた人がいるなら、それで十分だと思う。
解けなくてもいい。証明できなくてもいい。
でも、「これは面白い」と感じたなら――
あなたもすでに、この問いの読者であり、共同者なのだ。
■ 最後に
私たちは今、AIとともに問いを生み出せる時代に生きている。
それは答えを得るより、ずっと重要なことかもしれない。
次回:この命題が持つ数論的な構造と、“ズレた次元”が生み出す可能性について掘り下げていきます。
コメントを残す