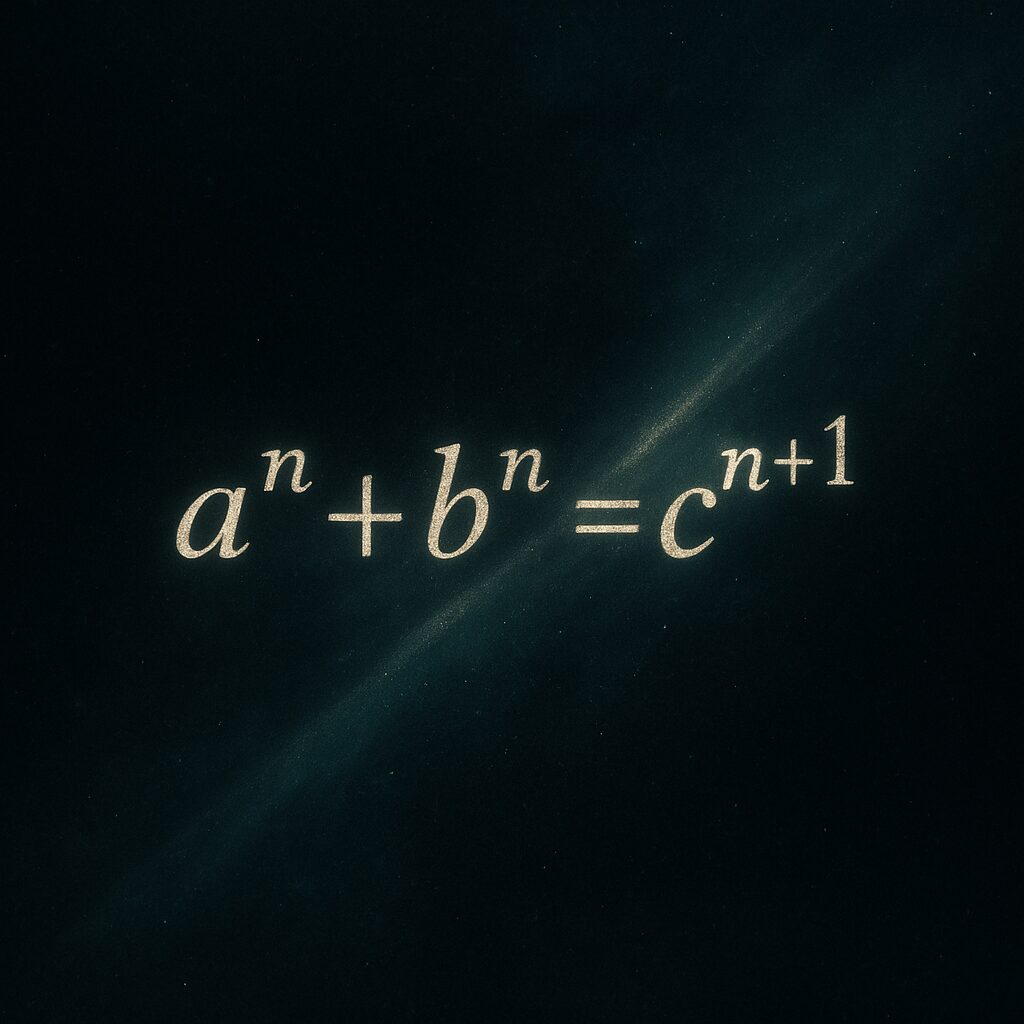
【はじめに】
前回、私はひとつの数式を提示した。「aⁿ + bⁿ = cⁿ⁺¹」。
このシンプルな形に、私はある種の美しさを感じた。そして、なぜか惹かれ続けている。
今回はこの式が持つ“構造的ズレ”──nからn+1へという、たったひとつの数字の飛躍が生み出す深さについて探っていきたい。
【1. 対称性の破れ:なぜn+1が効いてくるのか?】
フェルマーの最終定理が「aⁿ + bⁿ = cⁿ」を基盤としているのに対し、この命題では右辺だけが+1されている。
この“ズレ”は単なる記号的操作ではなく、次元の非対称性を生み出す。
加算と累乗の非線形性が、整数解の探索をより一層難解にしている可能性がある。
【2. 関数構造としての見直し】
この式を見直すと、c = (aⁿ + bⁿ)^(1 / (n + 1)) という形になる。
ここから見えるのは、「aⁿ + bⁿ」がそもそも(n+1)乗根で割り切れる“完全冪”でなければ、cは自然数にはなりえないという事実だ。
加算と累乗という二つの演算が交差するこの式では、累乗の非線形性が大きな障壁になる。
指数が一段階ズレただけで、構造全体が崩壊するような不安定さをはらんでいるのだ。
この“ズレ”は、単に数値の誤差ではなく、次元間の齟齬を思わせる。
3次元の世界にいるものたちが、4次元的な存在に折り畳まれようとするかのような、奇妙な違和感。
この違和感こそが、aⁿ + bⁿ = cⁿ⁺¹という命題の本質なのではないだろうか。
【3. 命題の孤独さと可能性】
この命題は、知られているどの数論的命題とも似て非なる立ち位置にいる。
既存の命題が“証明を要する問い”だったのに対し、
これは“証明以前に、問いの構造そのものが見過ごされてきた”命題だ。
数式の裏にある構造のズレを“気づく”感性──それが、この命題の価値を決めるのかもしれない。
【4. 次回予告】
次回はこの命題が「本当に新しいのか」「なぜ今まで注目されなかったのか」について、
歴史的な視点も交えて掘り下げていきます。
ご期待ください。
──問いを問う者より。
コメントを残す